โดยทั่วไป ผมจะคิดว่า ความพิเศษของเดือน ก.พ. คือ วันที่ 29 ก.พ.
(ปีที่เดือน กุมภาพันธ์ มี 29 วัน คือ ปี ค.ศ. ที่หารด้วย 4 ลงตัว)
เช่น ปี ค.ศ. 2024 (พ.ศ. 2567)
2024 ÷ 4 = 506 ลงตัว
และปีต่อไป คือ ค.ศ. 2028 (พ.ศ. 2571)

แต่ที่จริง มีเงื่อนไขเพิ่มเดิมอีกนิดหน่อย คือ
ถึง ปี ค.ศ. นั้นจะ ÷ ด้วย 4 ลงตัว แต่ถ้า ÷ ด้วย 100 ลงตัวด้วย
เช่น ปี ค.ศ. 1900 (พ.ศ. 2443)
1900 ÷ 4 = 475 ลงตัว
1900 ÷ 100 = 19 ลงตัว
แต่เราจะพบว่า ก.พ. 2443 มี 28 วัน
นั่นเพราะ ปี ค.ศ. นั้น ต้อง ÷ 400 ลงตัวด้วย จึงจะมี ก.พ. 29 วัน
(ถึงหารด้วย 4 และ หารด้วย 100 ลงตัว แต่ 1900 ÷ 400 = 4 เหลือ เศษ 300)

สรุป คือ ต้อง ÷ ด้วย 4 ลงตัว และ ถ้า ÷ ด้วย 100 ลงตัวด้วย ต้อง check อีกครั้ง ด้วยการ ÷ ด้วย 400 ลงตัว จึงจะเป็นปีที่มี ก.พ. 29 วัน ครับ
เช่น ปี ค.ศ. 2000 (พ.ศ. 2543)
2000 ÷ 4 = 500 ลงตัว
2000 ÷ 100 = 20 ลงตัว
ต้อง check ด้วยการ ÷ ด้วย 400 อีกครั้ง
2000 ÷ 400 = 5 ลงตัว
เพราะฉะนั้น ปี พ.ศ. 2543 มีเดือน ก.พ. 29 วัน

นอกจาก วันที่ 29 กุมภาพันธ์ เดือนนี้ยังเคยเป็นชื่อ ภาพยนตร์ในความทรงจำ อีกเรื่องนึง (นานมากๆ) เป็นเรื่องสร้างชื่อของ คุณ เจี๊ยบ โสภิตนภา นักแสดงนำ

จนมาในปีนี้ พ.ศ. 2569
ลูกน้อง ฉีกปฏิทินเดือน มกราคม ออก ทำให้ผมรู้สึกประหลาด เมื่อมองที่เดือนใหม่
กุมภาพันธ์ มี 28 วัน ก็เหมือนปีที่แล้ว แต่ วันที่ 1 ก.พ. เริ่มที่ วันอาทิตย์ แล้วไปจบเดือนที่ 28 ก.พ. ที่วันเสาร์
ทำให้จำนวนวัน ใน wk ครบจำนวน 7 วัน ใน 4 wk พอดีเป๊ะ
มองดูแล้วเป็นเดือนที่ “เต็ม” มาก

ทำให้ผมลองมองย้อนหา ก.พ. ในปี ที่มีลักษณะแบบนี้
พบว่า ที่ใกล้สุดที่เพิ่งผ่านมา คือ ปี ค.ศ. 2015 (พ.ศ. 2558)

ส่วนปีถัดไป ที่จะมี ก.พ. แบบนี้อีก คือ ปี ค.ศ. 2037 (พ.ศ. 2580)

และ ถ้าดูย้อนหลังไปถึงปี ค.ศ. 2000 (พ.ศ. 2543) จะพบ ก.พ. ที่เต็ม wk ในปีต่อไปนี้
2552 <—> 2558 <—> 2569 <—> 2580
ระยะห่างของแต่ละปีจะเป็น
+6 , +11, +11 , ….
คือ เริ่ม +6 แล้ว +11 , +11 จากนั้นจึงกลับมา +6 อีกรอบ
(6 + 11 + 11 = 28 –> 28 คือ ค.ร.น. ของ 4 และ 7, 4 มาจาก เดือนกุมภาที่ 4 ปี จะมี 29 วัน และ 7 คือ วันใน 1 wk )
ลอง check ดู ถ้าเป็นปี 2580 + 11 = 2591 (ค.ศ. 2048)

ที่ถูกต้อง ปีถัดไปคือ ปี ค.ศ. 2043 (พ.ศ. 2586) (จาก พ.ศ. 2580 + 6 = 2586)

ถ้าต้อง เพิ่มทีละ 6 ปี หรือ 11 ปี เป็นไปได้หรือไม่? ที่เราจะสร้างสมการ เพื่อคำนวณหา ปี ค.ศ. ที่มีเดือน ก.พ. แบบนี้
น่าจะเป็นไปได้นะ เพราะ ผมต้องการเงื่อนไขแค่ 2 ข้อ
คือ
- เดือน ก.พ. ในปีนั้น ต้องมี 28 วัน (เพื่อให้พอดี กับ wk เพราะ 28 ÷ 7 ลงตัว แต่ 29 ÷ 7 ไม่ลงตัว)
2. วันที่ 1 ก.พ. ต้องตรงกับ วันอาทิตย์
ผมจึงลองใช้วิชาพีชคณิตพื้นฐาน เพื่อสร้างสมการย้อนกลับ
โดยใช้ข้อมูล คือ ปี ค.ศ. ที่มีเดือน ก.พ. 28 วัน และ วันที่ 1 ก.พ. ต้องเป็นวันอาทิตย์
ตามที่กำหนดไว้ข้างต้น

สมการที่มีในใจ คือ ต้องเป็นตัวแปรที่มีการหารด้วย 4 เป็นส่วนประกอบ และมีผลรวมของ ปี ค.ศ. และส่วนประกอบ เป็นจำนวนรวม ที่หารด้วย 7 แล้วเหลือเศษ ที่ไม่ลงตัว
จากรูป ได้
(4 + x + y) -7z = 1
x = ปี ค.ศ. เช่น ปี 2026 –> x = 26
y = x หารด้วย 4 โดยไม่สนใจ เศษที่เหลือ เช่น x = 26
26 หาร 4 = 6 เศษ 2
y = 6
z = (4+x+y) หารด้วย 7 โดยไม่สนใจเศษที่เหลือ
เช่น 4+x+y = 4+26+6 = 36
36 หารด้วย 7 = 5 เศษ 1
z = 5
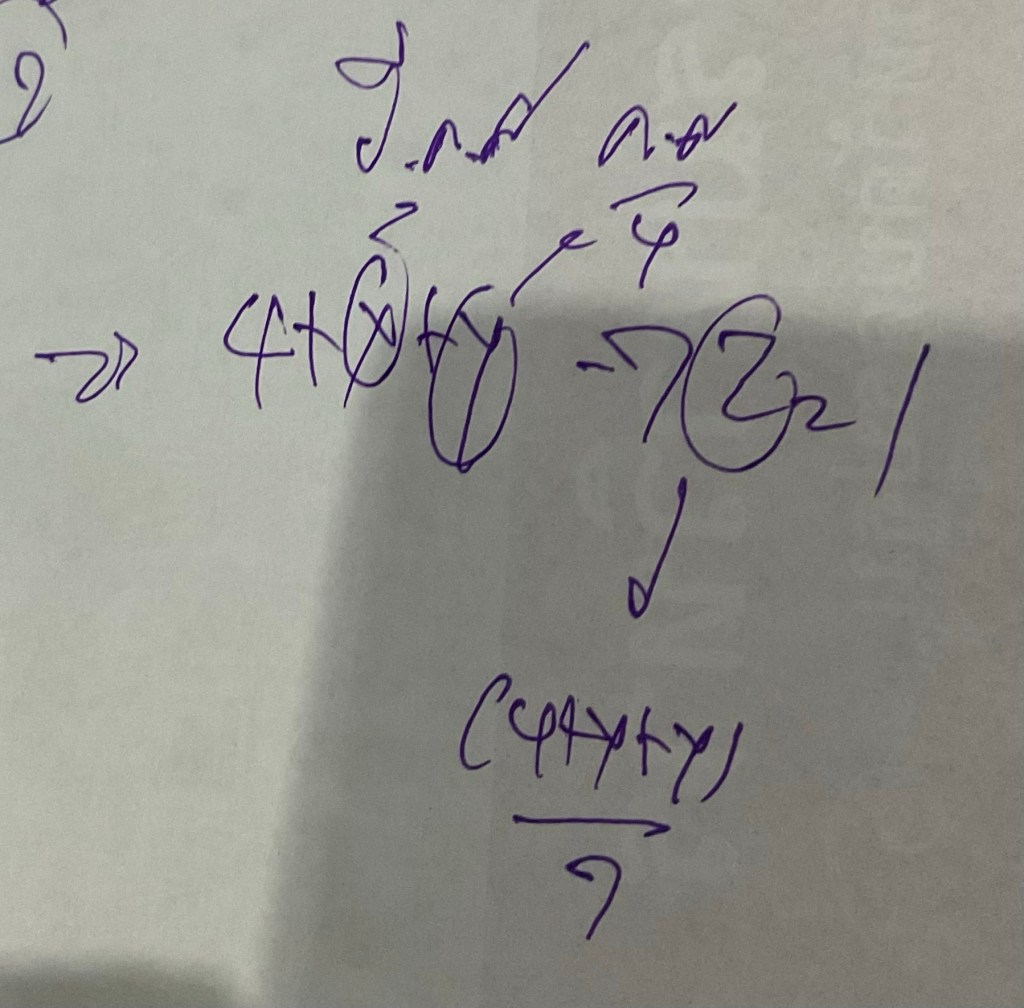
แทนค่าในสมการ
(4+x+y) – 7z = 1
(4+26+6) – 7(5) = 36 – 35 = 1
เพราะฉะนั้น ปี ค.ศ. 2026 (พ.ศ. 2569) เป็น ปีที่มีเดือน ก.พ. 28 วัน และ 1 ก.พ. เป็น วันอาทิตย์ ตามเงื่อนไข
และถ้าเราจัดรูปใหม่
4+x+y-7z = 1
x+y+3 = 7z
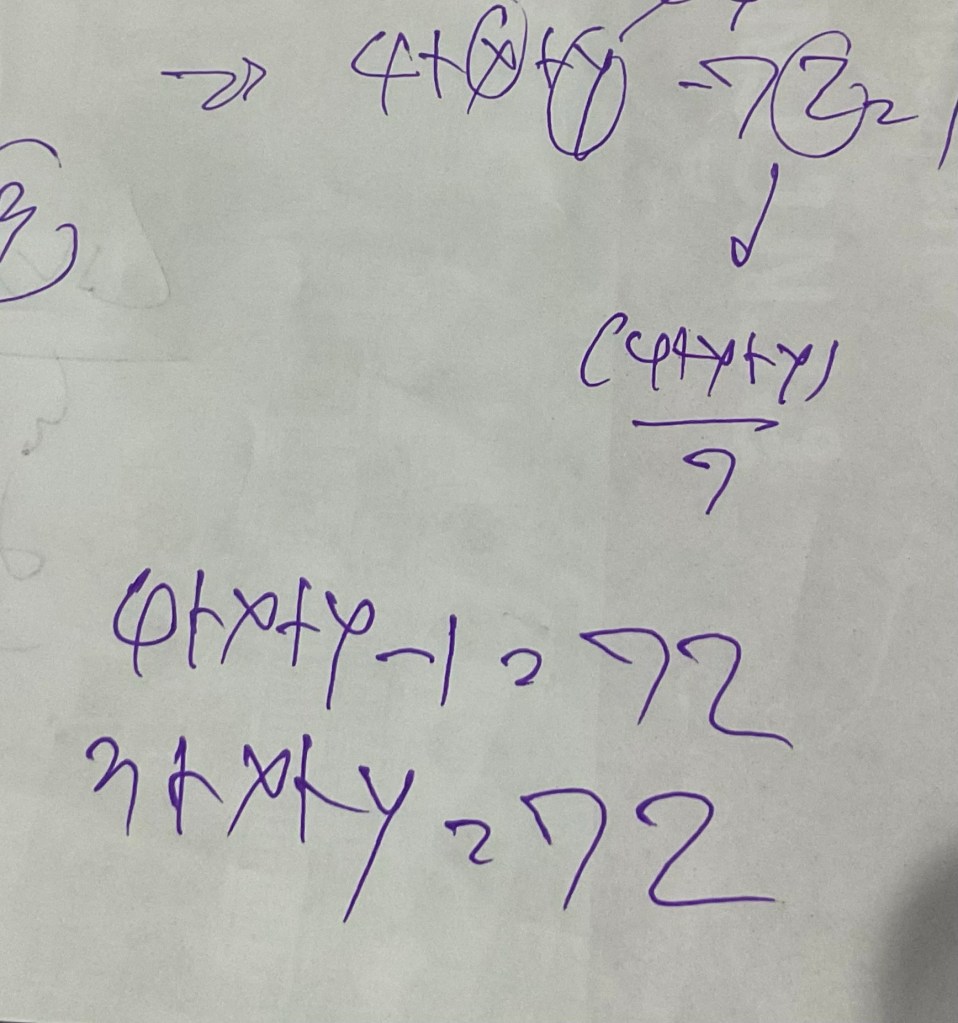
(x+y+3) ÷ z = 7
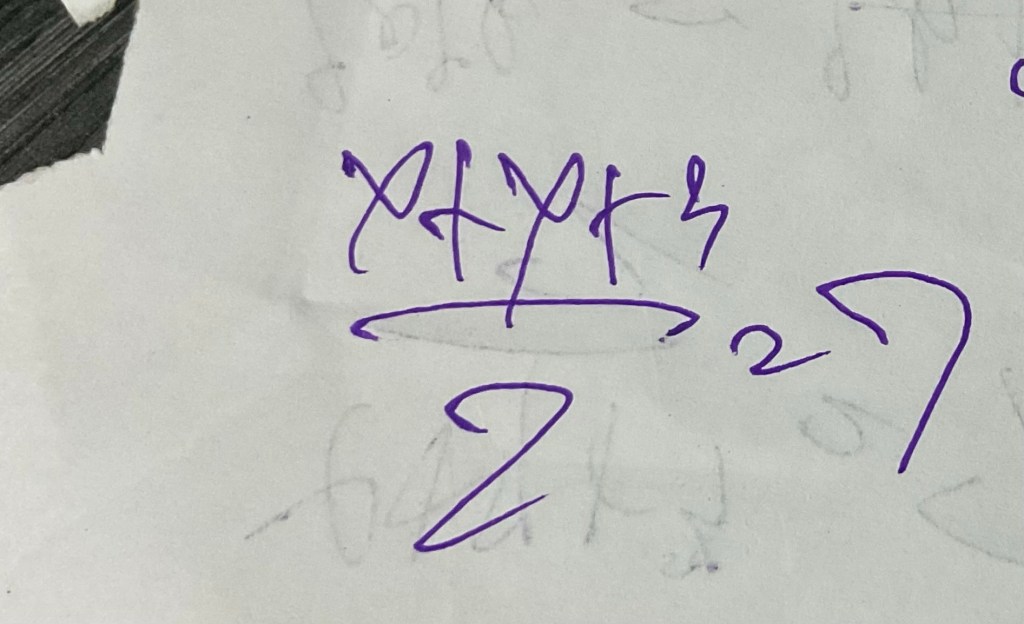
วิธีนำสมการนี้ไปใช้ คือ
นำปี ค.ศ. มาหาค่า x และ y
จากนั้น นำ x + y + 3
ถ้าผลรวมที่ได้ ÷ ด้วย 7 ลงตัว ปี ค.ศ. นั้น จะเป็นปีที่เรามองหา นั่นเองครับ
เช่น ปี พ.ศ. 2569 (ค.ศ. 2026) → x = 26, y = 6
x + y + 3 = 26 + 6 + 3 = 35 → 35 ÷ 7 ลงตัว → ปีนี้ จึงมี กุมภาพันธ์ แบบเต็ม wk
ปี พ.ศ. 2586 (ค.ศ. 2043) → x = 43, y = 10
x + y + 3 = 43 + 10 + 3 = 56 → 56 ÷ 7 ลงตัว → ปีนี้ จึงมี กุมภาพันธ์ แบบเต็ม wk
ปี พ.ศ. 2591 (ค.ศ. 2048) → x = 48, y = 12 (จริงๆ ตรงนี้ ทำให้เรารู้ได้แล้วว่า ไม่ใช่ เพราะ 48 ÷ 4 ลงตัว)
x + y + 3 = 48 + 12 + 3 = 63 → 63 ÷ 7 = 9 ลงตัว → ปีนี้ มีเดือน กุมภาพันธ์ ที่ ÷ 4 ลงตัว จึงมี 29 วัน เป็น กุมภาพันธ์ แบบไม่เต็ม wk

แต่ถ้าใครที่ตั้งให้วันแรกของ wk เป็นวันจันทร์ (ไม่ใข่วันอาทิตย์)
แบบนี้นะครับ วันแรกสุดของแต่ละ wk เป็น วันจันทร์

สมการ จะเปลี่ยนรูป นิดหน่อย เป็น
(4 + x + y) – 7z = 2
x + y + 2 = 7z
(x + y + 2) ÷ z = 7
นั่นคือ นำค่า x + y + 2 แล้ว ÷ ด้วย 7
ถ้า ผลหารลงตัว เดือน ก.พ. ของ ปีนั้น จะเต็ม wk ครับ (เริ่ม wk ด้วยวันจันทร์ นะ)
เช่น ปี พ.ศ 2569 (ค.ศ. 2026)
x = 26, y = 6 → x + y + 2 = 26 + 6 + 2 = 34 → 34 ÷ 7 ไม่ลงตัว → ปีนี้ ก.พ. ไม่เต็ม wk
ปี พ.ศ. 2570 (ค.ศ. 2027)
x = 27, y = 6 → x + y + 2 = 27 + 6 + 2 = 35 → 35 ÷ 7 ลงตัว → ปีนี้ ก.พ. เต็ม wk

สรุป โดยทั่วไป ถ้าปฎิทินตั้งค่า วันอาทิตย์ เป็นวันแรกของ wk
ใช้สูตร หา กุมภาพันธ์ แบบเต็ม wk จาก
(x + y + 3 ) ÷ 7 ได้ลงตัว (เหลือเศษเป็น 0)
x = ปี ค.ศ.
y = x ÷ 4 (ไม่คิดเศษ)
การคิดเป็นรายปี เสร็จสิ้นแล้ว
และ ถ้าเราอยากรู้ ลำดับ ว่า ปีไหน ที่จะลง lock เดือน ก.พ. แบบเต็ม wk ล่ะ?
วิธีที่ตรงที่สุด คือ ให้คิดย้อนกลับ หรือ ไปข้างหน้า
โดย -6 ปี หรือ -11 ปี ( กรณีนับไปในอนาคต คือ +6 หรือ +11 เช่นกัน)
แล้วนำผลที่ได้ มาเข้าสมการ check x+y+3 ว่า ผลรวม หารด้วย 7 ลงตัวหรือไม่?
ลงทดสอบ ถ้าให้ปี พ.ศ. 2569 (ค.ศ. 2026) เป็นปีที่มี ก.พ. เต็ม wk
ถ้าย้อนหลังไป 6 ปี –> พ.ศ. 2569 (2026) – 6 = พ.ศ. 2563 (2020)
เข้าสมการ x+y+3 = 20+ 5+ 3 –> พบว่า เป็นปีที่หารด้วย 4 ลงตัว –> ไม่ใช่ปีนี้แน่นอน
จึงต้องย้อนหลังไป 11 ปีครับ
—> พ.ศ. 2569 (2026) – 11 = พ.ศ. 2558 (2015)
เข้าสมการ x+y+3 = 15 + 3 + 3 = 21 –> 21 หารด้วย 7 ลงตัว —> ปีนี้มี ก.พ. เต็ม wk

ด้วยวิธีเดียวกัน
พ.ศ. 2558 (2015) – 6 = พ.ศ. 2552 (2009) –> 9 + 2+ 3 = 14 หารด้วย 7 ลงตัว
ปีนี้ จึงมี ก.พ. เต็ม wk

เราได้ 2552 <—> 2558 <—> 2569
และ จาก ปี พ.ศ. 2569
ถ้า +6 –> พ.ศ. 2569 (2026) + 6 = พ.ศ. 2575 ( 2032)
x+y+3 = 32 + 8 + 3 –> พบว่า เป็นปีที่หารด้วย 4 ลงตัว จึงไม่ใช่ปีนี้
ต้อง +11 –> พ.ศ. 2569 (2026) + 11 = พ.ศ. 2580 ( 2037)
check ค่า x+y+3 = 37 + 9 + 3 = 49 –> หารด้วย 7 ลงตัว —> ปีนี้ถูกต้อง มี ก.พ. เต็ม wk ครับ

ต่อไปผมลองคิดไปเรื่อยๆ
2580, 2586, 2597, 2608, 2614, 2625, 2636, 2642
เวลาของปีที่ + เพิ่ม จะเป็นลำดับดังนี้
+6, +11, +11, +6, +11, +11, +6
ถ้าดูแบบนี้ ลำดับปีต่อไปน่าจะเป็น +11 คือ พ.ศ. 2642 + 11 = พ.ศ. 2653 ใช่มั๊ยครับ?
แต่ กลับไม่ใช่อย่างที่คิดครับ คือ ตรงนี้ต้องเริ่มนับที่ +6 ใหม่ครับ (ไม่ใช่ +11)
เหตุผลเพราะ เมื่อถึงปี ค.ศ. 2099 (พ.ศ. 2642) จะเข้าสู่ ศตวรรษใหม่ คือ เริ่ม ค.ศ. 2100 ( พ.ศ. 2643)
การเรียงลำดับจะเริ่มใหม่คือ
+6, +11, +11, +6, +11, 11, … ไปเรื่อยๆ จนครบอีก 100 ปี ครับ
2648, 2654, 2665, 2676, 2682,
แสดง เดือน ก.พ. พ.ศ. 2648 ( ค.ศ. 2105)

ซึ่งตั้งแต่ปี ค.ศ. 2100 (พ.ศ. 2643) สมการ x+y+3 จะใช้ไม่ได้แล้ว ต้องเปลี่ยนเป็น x+y+1 แทน (จะมีท่านผู้อ่านอยู่นี้ ได้ใช้สมการนี้มั๊ย?)
สมการ x+y+3 จะใช้ได้แค่ 100 ปีครับ คือ ค.ศ. 2000 (พ.ศ. 2543) – ค.ศ. 2099 (พ.ศ. 2642)
ลอง check ปี ค.ศ. 2122 ( พ.ศ. 2665) คือ อีก 99 ปีข้างหน้า
แทนค่า x+y+1 = 22 + 5 + 1 = 28 –> 28 หารด้วย 7 ลงตัว ปีนี้ เดือน ก.พ. จึงครบ wk ครับ

เราอาจอยู่ไม่ถึงวันนั้น แต่เรารู้ถึงมันได้
Ref: